Public Events

Public Events


Quantum Geometry at a DAMTP Open Day, Cambridge
A presentation of my work at an Open Day at the Department of Applied Mathematics and Theoretical Physics, University of Cambridge in the days when my research group was based there.
Quantum geometry is a radical new concept of geometry that goes much beyond our usual concepts of flat or even of curved spacetime, being powerful enough to not break down in the quantum world. From school you should recall that at a subatomic scale the world is `fuzzy' or `wavelike', as expressed by Heisenberg's famous uncertainty principle. This says that one cannot know both the position and the velocity (or, more precisely, the momentum) of an electron at the same time. The product of their uncertainties must exceed Plancks constant 0.0000000000000000000000623 in usual metric units. There are many ways to see the origin of this uncertainty. One is that when you try to measure a quantum system you inevitably disturb it; in particular you cannot measure both the position and momentum of a quantum particle at the same time. As soon as you measure one you invalidate your previous measurement of the other.
This is obviously far removed from our usual macroscopic ideas of particles as moving about with some definite position and velocity. Those Newtonian ideas of classical geometry work very well at medium and large scale, but the subatomic quantum world simply is not like that. One needs a new kind of `quantum geometry' more appropriate to this domain of nature.
Looking closely at the Heisenberg uncertainty relations, one sees their origin in the relations xp-px=ih where h is the above Planck's constant. Here x,p are the quantum operators which play the role of position and momentum variables in usual macroscopic physics. Because xp is not px, one cannot measure both x,p simultaneously. It matters in which order we measure! Note that the particular form of the relations does not matter -- we have similar phenomena whenever xp and px do not coincide. For some modern variants of Heisenberg's relations one may even have an absolute minimum uncertainty for x or for p separately.
Quantum geometry is founded on this idea that the order of measurement matters. It takes the view that all geometric `coordinates' in the quantum world may be potentially of this type where the order matters. Let us look at this in more detail.
One of the simplest examples of a quantum geometry is the quantum plane. Usually, a plane is described by two co-ordinate functions x,y. Of course, the functions xy and yx are the same since it does not matter whether you measure x first and then y or y first and then x. This is what you lose in the quantum world. It's an effect that you do not see in macroscopic physics.

Here xy=yx for all points P. This is lost in quantum geometry
In the quantum plane we replace the property xy=yx by xy=qyx where q is a parameter. We do not have points any more but we can continue to work algebraically with x and y. Many quantum spaces are known, including quantum groups and braided groups.
We can really do geometry in this setting where co-ordinates do not commute. This is the remarkable discovery in the last few years. For example, we can follow the approach of Isaac Newton and define differentiation by
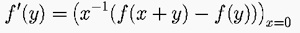
But when xy is not yx, this does not give the answer Newton found! If yx=qxy we get instead
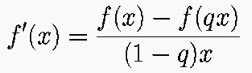
which shows that quantum geometry replaces the smooth continuum assumed in Newtonian calculus by finite differences. We also have integration in quantum geometry, with
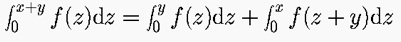
Do these formulae remind you of high school calculus? They should do, but x,y,z are not usual variables as yz=qzy, etc. All the usual structures of geometry have been built up over the last few years in this quantum setting.
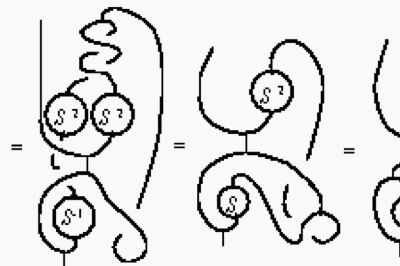
Braided independence is another of the conceptual ideas going into the modern approach to quantum geometry. When electrons pass each other either in physical space or lexicographically during a calculation, their exchange involves an additional -1 factor. Building on this idea, one is led to a kind of braided mathematics in which the outputs of calculations are `wired' into the inputs of further calculations much like the way information flows inside a computer. Only now, when wires cross each other there is a nontrivial operator, in fact a different one for when one wire goes under the other and when it goes over. Here is a typical calculation in braided-mathematics

Proof of translational invariance of integration in braided mathematics
Clearly, this aspect of the work is right on the frontier of pure mathematics, as well as being needed for quantum physics.
Wednesday, 30 September 1998