Public Events

Public Events


A Web Essay on Physics v Mathematics
This is an essay on my philosophical ideas on `The Nature of Physics’ that think I first put up on my website when I was based in DAMTP (the above date of entry is a bit of an estimate from this).
The goal of theoretical physics, at least in my opinion, is to arrive at our best understanding of the fundamental processes of nature. We use of course the language of mathematics, and most physicists (including me) would ideally like to find a single elegant theory powerful enough in principle to explain all known phenomena. In practice it means our existing domains of understanding should be recovered as special limits. Personally, I would go a bit further and say that ideally, on my deathbed, I would like to have reached the `right point of view' whereby it was all obvious, why the world had to be that way. If I was religious (I'm not), I guess I would be Buddhist and this would be nirvana.
There is obviously an element of philosophy to this quest and, while I do not think that philosophy per se should be confused with theoretical physics, one can still think about the `big picture' and have views that sit in the background and underly or motivate ones actual research. This page contains some of my thoughts about this bigger picture. I am not a qualified philosopher, so take it as my opinion only.
In a nutshell, the idea that has influenced me most in my actual research work is the principle that there is a deep duality or `conceptual Fourier transform' between theory and experiment, between abstract laws and measurement. More details are given in the paper S. Majid, Principle of representation-theoretic self-duality, Phys. Essays. 4 (1991) 395-405, where the thesis presented is (roughly speaking) that physics polarises down the middle into two parts, one which represents the other, but that the latter equally represents the former, i.e. the two should be treated on an equal footing.
The starting point is that Nature after all does not know or care what mathematics is already in textbooks. Therefore the quest for the ultimate theory may well entail, probably does entail, inventing entirely new mathematics in the process. In other words, at least at some intuitive level, a theoretical physicist also has to be a pure mathematician. Then one can phrase the question `what is the ultimate theory of physics ?' in the form `in the tableau of all mathematical concepts past present and future, is there some constrained surface or subset which is called physics ?' Is there an equation for physics itself as a subset of mathematics? I believe there is and if it were to be found it would be called the ultimate theory of physics. Moreover, I believe that it can be found and that it has a lot to do with what is different about the way a physicist looks at the world compared to a mathematician (so yes, I too spend an inordinate amount of time at dinner parties debating this interesting question).
To begin with, theoretical physics is not so much concerned with `what' is observed but with the question `why is it observed?'; i.e. it always seeks to explain structures in terms of still more fundamental structures or principles. This reductionist programme takes the naive view that there are indeed some fundamental laws of nature, of which our experiments and observations are representations. Thus it is supposed that something is absolutely true, and that something else measures or observes it. However, one of the themes one can explore is that such evaluations should generally be thought of more symmetrically as a `duality pairing' of one structure with another. An evaluation f(x) can also be read x(f), where f is an element of a dual structure. Since theoretical physics adopts the language of mathematics, such an `observer-observed' reversed interpretation of the mathematical structure can always be forced, but will the dual interpretation also describe physics? It is exactly the idea that the answer should be `yes' which led to some of the first Hopf algebras (quantum groups), namely as quantum systems exhibiting an observable-state self-duality (see the paper S. Majid, Hopf algebras for Physics at the Planck scale J. Class. Quant. Grav. 5 (1988) 1587-1607). We can then try to elevate the idea to a more general principle of representation-theoretic self-duality, that a fundamental theory of physics is incomplete unless such a role-reversal is possible. We can go further and hope to fully determine the (supposed) structure of fundamental laws of nature among all mathematical structures by this self-duality condition.
Such duality considerations are certainly evident in some form in the context of quantum theory and gravity. The situation is summarised to the left in the following diagram. For example, Lie groups provide the simplest examples of Riemannian geometry, while the representations of similar Lie groups provide the quantum numbers of elementary particles in quantum theory. Thus, both quantum theory and non-Euclidean geometry are needed for a self-dual picture. Hopf algebras (quantum groups) precisely serve to unify these mutually dual structures. One finds, at least in some specific models that imposing the duality requirement in the context of particles moving on homogeneous spaces forces the homogeneous spaces to come in mutually dual pairs, and, moreover, constrains the allowed effective metric and dynamics in a way not too unlike Einstein's equations in this context. More recently, the notion of T-duality in string theory should probably be viewed as a further manifestation of this idea (a nice research project to make this precise...)
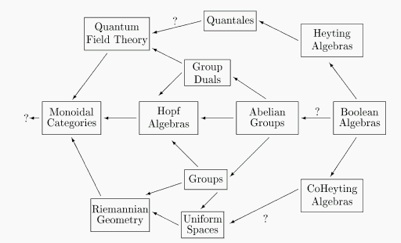
If this principle is right, we should be able to use it as a guide to the required mathematical structure for the next more advanced theory of quantum mechanics and gravity. There are two steps, the first being to identify or invent the relevant self-dual category or axiom-system beyond Hopf algebras but with similar input--output symmetry or self-duality properties of the axioms. The second step would be to construct some concrete models in such a framework. The long-term aim is to have in this way a picture of the full Einstein's equation on a general metric (i.e. not only homogeneous ones) appearing as a self-duality constraint. Recall that Einstein's equation does indeed equate a geometrical object (the Einstein tensor which measures the curvature of spacetime) to a quantum-mechanical object (the vacuum expectation of the stress energy tensor which measures the matter content).
We also note that, in addition to the `end' of theoretical physics in the form of quantum-gravity, we can ask also about its `birth'. We take the view that the simplest theories of physics are based on classical logic or, roughly speaking, Boolean algebras. It appears that the relevant duality here may be provided by complementation with Boolean algebras considered self-dual according to De Morgan's theorem. The situation is summarised on the right in the figure. Going above the axis to Heyting algebras and beyond takes us into intuitionistic logic and ultimately into an axiomatic framework for quantum field theory. A Heyting algebra describes logic in which one drops the familiar `law of the excluded middle' that either a proposition or its negation is true. This generalisation is also the essential feature of the logical structure of quantum mechanics. Dual to this is the notion of co-Heyting algebra and co-intuitionistic logic in which one drops the axiom that the intersection of a proposition and its negation is empty. It has been argued by F.W. Lawvere and his school that this intersection is like the `boundary' of the proposition, and, hence, that these co-Heyting algebras are the `birth' of geometry. The long-term programme at this end of physics is to develop this geometrical interpretation of co-intuitionistic logic further into the notion of metric spaces and ultimately into Riemannian or Lorentzian geometry.
In between these extremes, a well-known example of a self-dual category is that of (locally compact) Abelian groups. For every such group there is a dual one G^ of its representations. Especially important is that G^^ is isomorphic to G. The position and momentum groups in flat space are dual to each other in this way. Another example is for a particle on a circle, where the allowed momentum modes are labeled by the dual group Z. Fourier transform interchanges the roles of the group and its dual. This familiar setting gives a clue to the philosophical basis of the principle of representation-theoretic self-duality. For if some theorist thought that a group G was the `true' structure underlying a law of physics and that G^ was its representations, a more experimentally-minded physicist might equally well consider G^ as the true object and G as its representations. Only in a self-dual category could both points of view be entertained. This says that the principle has its origins in the nature of the scientific method. If, for example, Einstein's equation and other laws of theoretical physics could be deduced from such a principle alone, we would have achieved a Kantian or Hegelian view of the nature of physical reality as a consequence of the choice to look at the world in a certain way. Of course, it's never going to be as simple as that, but it's something to think about on a rainy day.
1 September 1997