Deterministic chaos and
nonequilibrium statistical mechanics:
outline of contents
-
0.
-
Introduction
-
list of references
-
table of contents
-
overview: models and key ideas
-
1.
-
Basic concepts of dynamical systems theory
-
deterministic chaos in piecewise linear maps
-
Lyapunov exponents, dynamical entropies, and fractal dimensions
-
probability measures and the Frobenius-Perron equation
-
2.
-
Chaotic diffusion
-
random walks
-
diffusion equation and escape rate formalism
-
Green-Kubo formula and fractal functions
-
thermodynamic formalism
-
cycle expansion methods
-
anomalous diffusion
-
3.
-
Chaotic currents and chaotic reaction-diffusion
-
linear and nonlinear response in simple biased maps
-
Langevin equations, ratchets, and molecular motors
-
reaction-diffusion systems
-
4.
-
Disordered dynamical systems
-
quenched disorder and subdiffusion
-
diffusion on disordered lattices
-
chaotic diffusion and noise
-
5.
-
Chaotic transport in multibaker maps
-
ergodic properties, dynamical systems classifications, and time-reversibility
-
relation between one-dimensional maps and baker maps
-
diffusive multibaker maps
-
biased multibaker maps and entropy production
-
6.
-
Chaotic diffusion in the periodic Lorentz gas
-
definition of the model and dynamical properties
-
relation between the periodic Lorentz gas and two-dimensional maps
-
analysis of the density-dependent diffusion coefficient
-
Boltzmann equation, kinetic theory, and Lyapunov exponents
-
7.
-
the thermostated systems approach to nonequilibrium steady states
-
the Gaussian thermostated Lorentz gas
-
chaotic and fractal properties of nonequilibrium steady states in thermostated
systems
-
the Nose-Hoover thermostat, generalized Liouville equation, and generalized
Hamiltonian formalism
-
criticism of this approach
-
8.
-
the thermostated systems approach revisited
-
non-ideal Gaussian and Nose-Hoover thermostats
-
stochastic boundary conditions
-
thermostating by deterministic scattering
-
do there exist universal chaotic and fractal properties of thermostated
nonequilibrium steady states?
-
deterministic thermostats, active Brownian particles, and cell motility
-
9.
-
fluctuation theorems
-
10.
-
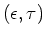 -entropies
and microscopic chaos in experiments?
-entropies
and microscopic chaos in experiments?