Network Geometry
HOME
BIOGRAPHY
RESEARCH
GROUP AND ALUMNI
CONTACT
BIOGRAPHY
RESEARCH
- MULTILAYER NETWORKS
- NETWORK GEOMETRY
- TEMPORAL NETWORKS
- NETWORK CONTROL
- BIANCONI-BARABASI MODEL
- CONDENSATION TRANSITIONS
- CRITICAL PHENOMENA ON NETWORKS
- SUBGRAPHS: LOOPS AND CLIQUES
- ENTROPIES OF NETWORK ENSEMBLES
- ENTROPIES FOR INFERENCE PROBLEMS
- BIOLOGICAL NETWORKS
GROUP AND ALUMNI
CONTACT
Network Geometry aims at characterizing discrete network structures as geometrical objects. In this context simplicial complexes, i.e. network formed by triangles, tetrahedra, etc.., play an important role. The advance in this field it is important for characterizing complex networks in the brain or in communication technology. At the same this emerging field is providing the ground for extablishing a cross-fertilization between complex networks and quantum gravity.
I have recently worked on emergent network geometry obtain results in different directions:- In Emergent Complex Network Geometry an growing simplicial complex formed by triangles is able, just with two parameters to generate either 2d manifols or scale-free networks, with high clustering coefficient, small-world diameter and significant modular structure.
-
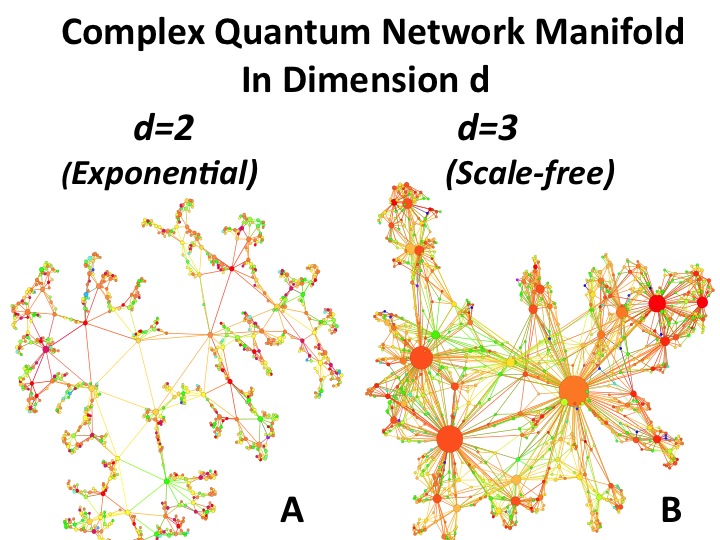
Complex Quantum Network Manifolds are emerging from a non equilibrium dynamics of simplicial complexes in arbitrary diemnsions. They are scale-free for any dimension greater than two. Interestingly their statistical properties are described by generalized degrees. In dimension 3 the generalized degree of the tringular faces, of the link and of the nodes follow respectively the Fermi-Dirac, the Boltzmann, and the Bose-Einstein distribution.
The paper has been widely covered by the press. - Network Geometry with Flavor is a general framework for emergent network geometry that includes the Bianconi-Barabasi model, and Complex Quantum Network Manifolds. Interestingly the model can be related to Regge calculus.
Selected publications
-
Z. Wu, G. Menichetti, C. Rahmede, G. Bianconi
Emergent Complex Network Geometry Scientific Reports 5, 10073 (2015). -
G. Bianconi and C. Rahmede,
Complex Quantum Network Manifolds in d>2 are Scale-Free
Scientific Reports 5, 13979 (2015).
(Covered in the press Science Daily,Phys.org,La Stampa,MEDIA INAF) -
G. Bianconi and C. Rahmede,
Network geometry with flavor:from complexity to quantum geometry
Physical Review E 93, 032315 (2016).
-
G. Bianconi,
Interdisciplinary and physics challenges in network theory
Europhysics Letters 111, 56001 (2015). -
G. Bianconi, C. Rahmede and Z. Wu,
Complex Quantum Network Geometries: Evolution and Phase Transitions
Phys. Rev. E 92, 022815 (2015). -
K. Zuev, M. Boguna, G. Bianconi,D. Krioukov,
Emergence of Soft Communities from Geometric Preferential Attachment, Scientific Reports 5, 9421 (2015).