Nonextensive Statistical Mechanics is a generalization of ordinary statistical mechanics,
based on the extremization of more general entropy measures than just the Shannon entropy.
These more general entropy measures are the so-called Tsallis entropies.
They depend on a real parameter q. For q=1 ordinary statistical mechanics is recovered.
For q different from 1 this is a kind of q-deformed version of statistical mechanics.

The more general formalism is in particular useful for the description of systems with long-range interactions,
multifractal behaviour, and fluctuations of temperature or energy dissipation rate. Examples of recent physical applications
are nonequilibrium systems with a stationary state (including turbulent flows), scattering processes in elementary particle
physics, and plasmas.

Quite a complete list of references on nonextensive statistical mechanics and its recent
successful applications can be found here.

Here is a recent popular science article in the Science magazine (23 August 2002) on this new approach.

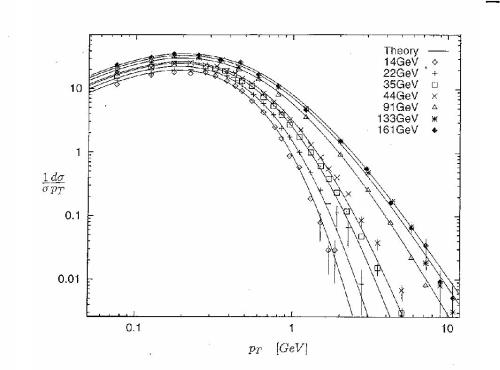
As an example, the following picture shows differential cross sections of hadronic particles
as produced in e+e- annihilation experiments.
The measurements were done by the TASSO and DELPHI collaboration.
Essentially the figure shows how many particles with a given transverse momentum p_T
are produced at a certain center-of-mass energy E. The solid lines
are analytical predictions of a model based on nonextensive statistical mechanics.
There is excellent agreement between theory and experiments.

Measurements by TASSO and DELPHI

More details can be found in
C. Beck, Non-extensive statistical mechanics and particle spectra in elementary interactions, Physica 286A , 164 (2000)
download ps file

Back to home page